Рекурсия в JavaScript — это процесс вызова самого себя. Функция, которая вызывает (invokes) саму себя, называется рекурсивной функцией. Другими словами, программа, в которой функция вызывает саму себя, называется рекурсией, а связанная с ней функция называется рекурсивной функцией.
Рекурсивная функция — это цепочка вызовов одной и той же функции. Это похоже на цикл с условием завершения или без него. Он вызывает сам себя, прямо или косвенно, через другую функцию.
Известным примером, часто используемым для описания рекурсии, является вычисление факториала (факториал для значения 5 равен 5 * 4 * 3 * 2 * 1).
Рекурсию в JavaScript лучше всего использовать, когда нам нужно многократно вызывать одну и ту же функцию с разными параметрами. Это дает программистам некоторые преимущества, такие как разработка аккуратного и короткого кода, а также помогает программистам избегать циклов.
- Синтаксис рекурсии JavaScript
- Как остановить рекурсию в JavaScript?
- Пример программы, основанной на рекурсии JavaScript
- Факториальная программа, использующая рекурсию в JavaScript
- Рекурсивный факториал
- Ряды Фибоначчи с использованием рекурсии в JavaScript
- Итеративное решение: ряд Фибоначчи
- Рекурсивное решение: ряд Фибоначчи
- Программа для написания каждой цифры отдельно
Синтаксис рекурсии JavaScript
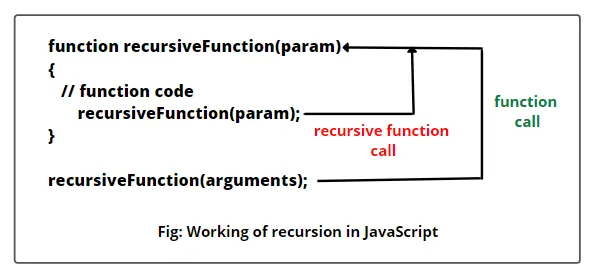
Синтаксис для объявления рекурсивной функции в JavaScript, которая вызывает саму себя напрямую, следующий:
function recursiveFunction(param) {
// function code
recursiveFunction(param);
}
recursiveFunction(arguments);Приведенная выше recursiveFunction() — это рекурсивная функция, которая вызывает саму себя внутри функции. Также возможно, что рекурсивная функция вызывает саму себя косвенно.
Синтаксис для объявления рекурсивной функции, которая неоднократно вызывает саму себя косвенным образом, выглядит следующим образом:
function recursiveFunction1(param) {
// function code.
recursiveFunction2(param);
}
function recursiveFunction2(param) {
// function code.
recursiveFunction1(param);
}
Предположим, нам нужно запустить функцию recursiveFunction() в приведенном выше коде. Каким будет результат? В этом случае приведенная выше recursiveFunction будет выполняться бесконечно. Из-за чего может произойти сбой веб-браузера.
Как остановить рекурсию в JavaScript?
При определении рекурсивной функции необходимо указать условие завершения. Если мы не укажем такое условие, то может произойти бесконечный вызов «функции».
По этой причине нам нужно установить условие для завершения рекурсии. Это условие называется базовым случаем или точкой остановки. Базовый случай — это условие, которое предотвращает бесконечную рекурсию. В базовом случае рекурсивных вызовов функций не происходит.
Рассмотрим следующий пример кода ниже.
function recursiveFunction(understandRecursion)
{
const recursAnswer = confirm("Do you understand recursion?");
if(recursAnswer === true) // base case or stopping point.
{
return true;
}
recursiveFunction(recursAnswer); // Recursive call.
}
В этом примере функция recursiveFunction() будет продолжать вызывать саму себя до тех пор, пока значение recursAnswer не будет равно true. В теле функции условный оператор используется для создания базового варианта.
Пример программы, основанной на рекурсии JavaScript
Давайте рассмотрим очень простой пример программы, основанной на рекурсии. В этом примере мы будем выводить числа с обратным отсчетом от 5 до 1. Посмотрите на следующий код скрипта.
Пример 1:
<html>
<head>
<title>Program to count down numbers to 1</title>
<script>
function countDown(num)
{
// Displaying the number
document.write(num, "<br>");
// Decreasing the number value by 1.
const newNum = num - 1;
// Base case or stopping point.
if (newNum > 0) {
countDown(newNum);
}
}
countDown(5); // calling function.
</script>
</head>
</html>
Вывод: 5 4 3 2 1
В приведенном выше коде мы передали число в качестве аргумента при вызове функции. В теле функции мы использовали условный оператор для проверки того, что переданный аргумент больше нуля.
Это базовое условие. Пока это условие имеет значение true, рекурсивная функция countDown() вызывает саму себя. На каждой итерации значение числа уменьшается на 1 и вызывается функция countDown() до тех пор, пока число не станет положительным.
Посмотрите на следующие шаги, чтобы более четко понять рекурсивные вызовы.
Обратный отсчет (5) выводит 5 и вызывает обратный отсчет (4) Обратный отсчет (4) выводит 4 и вызывает обратный отсчет (3) Обратный отсчет (3) выводит 3 и вызывает обратный отсчет (2) Обратный отсчет (2) выводит 2 и вызывает обратный отсчет (1) Обратный отсчет (1) выводит 1 и вызывает обратный отсчет (0)
Когда число достигает 0, условный оператор принимает значение false. Поскольку базовое условие выполнено, функция больше не вызывается.
Пример 2:
<html>
<head>
<title>Program to count down numbers to 0</title>
<script>
function countDown(num)
{
if(num < 0) // base case. Stop at 0.
{
return; // stop function.
} else {
document.write(num, "<br>");
countDown(num - 1); // count down 1.
}
}
countDown(5); // calling function.
</script>
</head>
</html>
Вывод: 5 4 3 2 1 0
Факториальная программа, использующая рекурсию в JavaScript
В этом разделе мы узнаем, как вычислить факториал числа с помощью метода рекурсии. Факториал числа n представлен через n!. Это результат умножения чисел a от 1 до n.
Например, факториал числа 4 представлен 4!. Оно равно 4 * 3 * 2 * 1, в результате получается 24. Общие шаги для вычисления факториала любого числа n, следующие: (n) * (n – 1) * (n – 2) * (n – 3) *….. * 1.
Давайте напишем код для вычисления факториала числа с помощью цикла.
Пример 3:
<html>
<head>
<title>Program to compute the factorial of a number using loop</title>
<script>
function fact(num)
{
if(num < 0)
return undefined;
let total = 1;
for(let n = num; n > 1; n--)
{
total = total * n;
}
return total;
}
document.write(fact(6));
</script>
</head>
</html>
Вывод: 720
В этом примере мы вычислили факториал, начиная с заданного num, и уменьшаем num до тех пор, пока он не примет значение 2, поскольку факториал 1 равен 1. Мы уже включили его в итоговую переменную. Факториал нуля также равен 1. Факториал отрицательных чисел не может быть вычислен.
Рекурсивный факториал
Теперь давайте перепишем функцию fact, используя рекурсию.
Пример 4:
<html>
<head>
<title>Program to compute the factorial of a number using recursion</title>
<script>
function fact(num)
{
if(num === 1 || num === 0) // base case.
{
return 1;
}
return num * fact(num - 1); // recursive call.
}
document.write(fact(6));
</script>
</head>
</html>
Вывод: 720
Давайте напишем алгоритм для вычисления факториала числа 6. Рекурсивный вызов для вычисления факториала числа 6 имеет вид:
- fact(6) возвращает 6 * fact(5)
- fact(5) возвращает 6 * 5 * fact(4)
- fact(4) возвращает 6 * 5 * 4 * fact(3)
- fact(3) возвращает 6 * 5 * 4 * 3 * fact(2)
- fact(2) возвращает 6 * 5 * 4 * 3 * 2 * fact(1)
- fact(1) возвращает 6 * 5 * 4 * 3 * 2 * 1.
- fact(1) или fact(0) возвращает 1. 1! равный 1 и 0! также 1.
Вначале вам может показаться, что рекурсивные функции сложнее, но с практикой в некоторых программах они становятся проще.
Ряды Фибоначчи с использованием рекурсии в JavaScript
Ряд Фибоначчи — это список бесконечных чисел, каждое из которых является суммой последних двух чисел (начиная с 1). Например, 1, 1, 2, 3, 5, 8, 13, 21,…….
Давайте напишем программу на JavaScript для печати 20-й части последовательности Фибоначчи.
Итеративное решение: ряд Фибоначчи
Давайте напишем JavaScript-код для рядов Фибоначчи, используя цикл for. Это итеративное решение.
Пример 5:
<html>
<head>
<title>Program to sum the Fibonacci series of a number using for loop</title>
<script>
function getFibo(num)
{
if(num <= 1)
return num;
let sum = 0;
last = 1;
lastlast = 0;
for(let i = 1; i < num; i++)
{
sum = lastlast+last;
lastlast = last;
last = sum;
}
return sum;
}
document.write("Sum of Fibonacci numbers: " +getFibo(10));
</script>
</head>
</html>
Вывод: Сумма чисел Фибоначчи: 55
Здесь мы использовали цикл for, чтобы отслеживать последние два элемента ряда Фибоначчи, и его сумма дает число Фибоначчи.
Рекурсивное решение: ряд Фибоначчи
Давайте напишем код JavaScript рекурсивно, чтобы получить последовательность чисел Фибоначчи.
Пример 6:
<html>
<head>
<title>Program to sum the Fibonacci series of a number using recursion</title>
<script>
function getFibo(num)
{
if(num <= 1) // base case.
{
return num;
} else {
return getFibo(num - 1)+getFibo(num - 2);
}
}
document.write("Sum of Fibonacci numbers: " +getFibo(10));
</script>
</head>
</html>
Вывод: Сумма чисел Фибоначчи: 55
Программа для написания каждой цифры отдельно
Давайте теперь рассмотрим еще один пример программы, основанной на рекурсивной функции в JavaScript. Предположим, у нас есть вводимое число, и затем нам нужно записать каждую цифру отдельно.
Например, у нас есть число 567 в качестве входных данных, и мы должны отобразить 5, 6 и 7 отдельно. Давайте напишем для него код JavaScript.
Пример 7:
<html>
<head>
<title>Program to spell each digit separately</title>
<script>
function spell_num(number)
{
if(number < 10) // base case.
{
document.write(number, "<br>");
} else {
spell_num(Math.floor(number/10)); // recursive call.
document.write(number % 10, "<br>");
}
}
spell_num(567);
</script>
</head>
</html>
Вывод: 5 6 7
В этом примере мы объявили функцию с именем spell_num(), которая принимает в качестве входных данных номер параметра. В теле функции функция проверяет, меньше ли число 10.
Базовый случай — это когда число, переданное в качестве входных данных, меньше 10. В результате функция вернет само число, а не вызовет рекурсивную функцию. Число будет отображаться непосредственно в виде выходных данных в веб-браузере. В этом случае рекурсивный вызов не произойдет.
Если число больше или равно 10, функция вызовет рекурсивно, как показано ниже, список и передаст ему частное от числа, деленное на 10.
Далее остаток от числа, деленный на 10, будет напечатан в качестве выходных данных в браузере. Поскольку мы хотим печатать числа в правильном порядке слева направо, мы сначала вызовем рекурсивную функцию, а затем выведем остаток.
Для числа 567 последовательность вызова функции spell_num следующая:
- функция spell_num(567) // функция, вызываемая с помощью ввода 567.
- функция spell_num(56) // функция, вызываемая с помощью ввода 56.
- функция spell_num(5) // функция, вызываемая с помощью ввода 5.
В этом руководстве мы обсудили рекурсию в JavaScript с некоторыми примерами программ. Рекурсия — это фундаментальная концепция программирования, которую мы можем использовать вместо цикла и во многих сложных программах. Если рекурсия кажется вам запутанной, не волнуйтесь. В начале вы можете это почувствовать, но с практикой рекурсия становится проще.